Os Euclidianos: Definição e Fórmulas

Você sabe o que é Área?

Área é a medida de uma superfície.

Vamos aprender como calcular a área de algumas Figuras Planas

1. Quadrilátero

É uma figura plana que possui todos os lados iguais.

A letra h representa a medida da altura (heigtht - que significa altura em inglês) que e a letra b representa a medida da base do quadrado (a base se escreve da mesma forma em inglês).

A área do quadrado, retângulo ou paralelogramo é calculada multiplicando-se a base pela altura, tal como na fórmula abaixo:

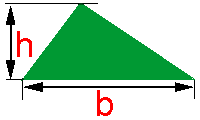
2. Triângulo

É um polígono de três lados.

A letra h representa a medida da altura (heigtht - que significa altura em inglês) que e a letra b representa a medida da base do triângulo (a base se escreve da mesma forma em inglês).

A área do triângulo é o valor da medida da base que multiplica o valor da medida da altura e divide por 2, tal como na fórmula abaixo:

3. Losango

Losango é um paralelogramo, cujas medidas dos lados são iguais e as diagonais são perpendiculares entre si. Ao decompor esta figura, você obtém quatro triângulos retângulos congruentes (iguais).

A área do losango é o valor da medida da diagonal maior que multiplica o valor da medida da diagonal menor e divide por 2, tal como na fórmula abaixo:

4. Trapézio

É uma figura que possui dois lados paralelos, correspondentes às suas bases uma maior e outra menor.

A área do trapézio é o valor da medida da base maior + a base menor que multiplica o valor da medida da altura e divide tudo por 2, tal como na fórmula abaixo: